[Machine Learning] 랜덤 포레스트(Random Forest)

앙상블(Ensemble)

여러가지 모델을 사용하여 Accuracy를 개선하는 방법

Ensemble의 종류

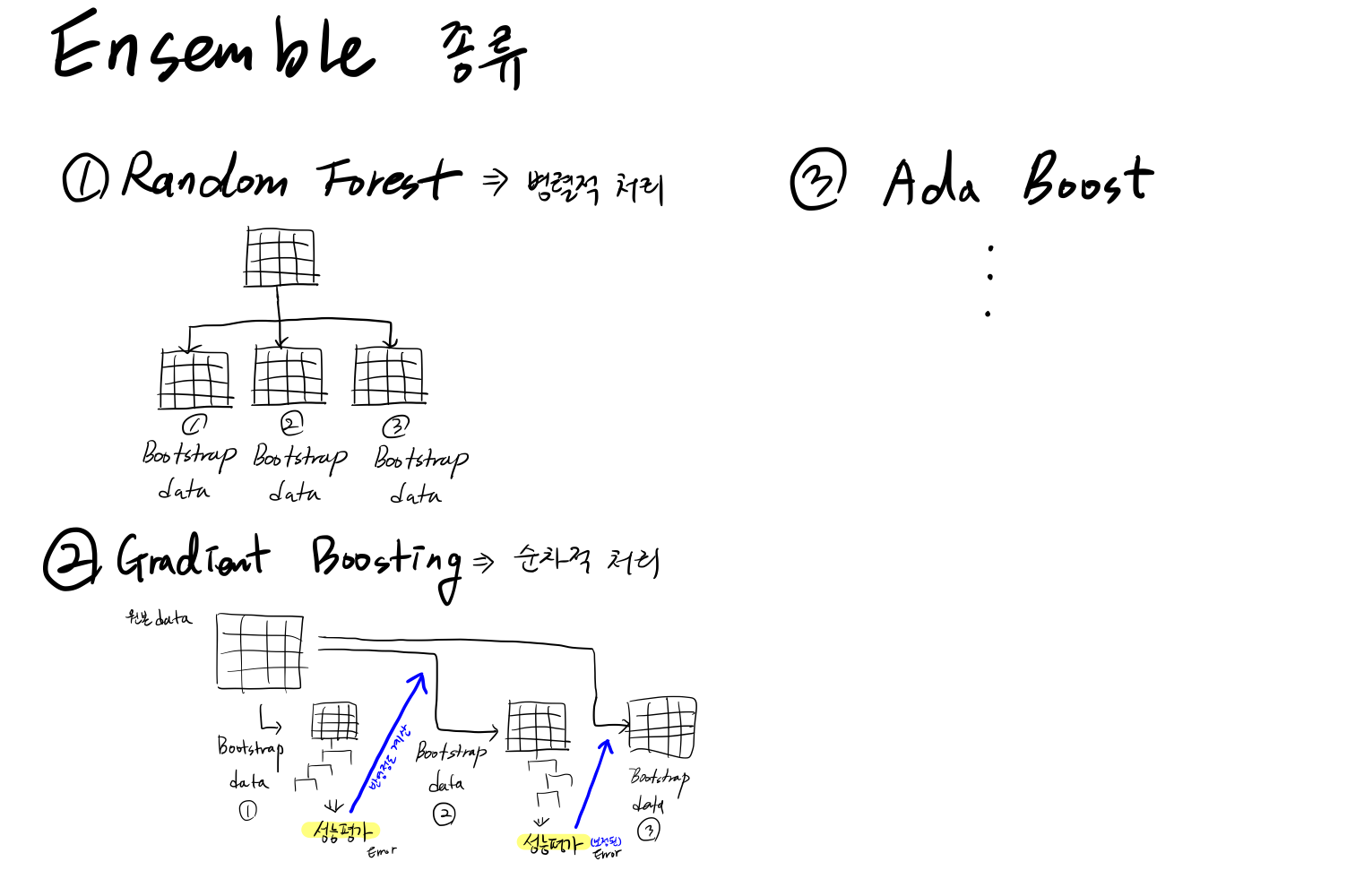
Random Forest(랜덤 포레스트)

의사결정나무(Decision Tree)의 앙상블(Ensemble)

• 의사결정나무에서 나무를 여러개 만드는 것
• 지도학습의 일종

특징

• 다수의 의사결정 나무들의 결과로부터 모델을 생성함
• 모델 생성 시 다양성(Diversity)과 임의성(Random) 부여
• 모델 Accuracy를 높이고 및 Overfitting 발생 가능성을 낮춤
• 일반적으로 의사결정나무 보다 성능이 좋음

1) 다양성(Diversity)과 임의성(Random)

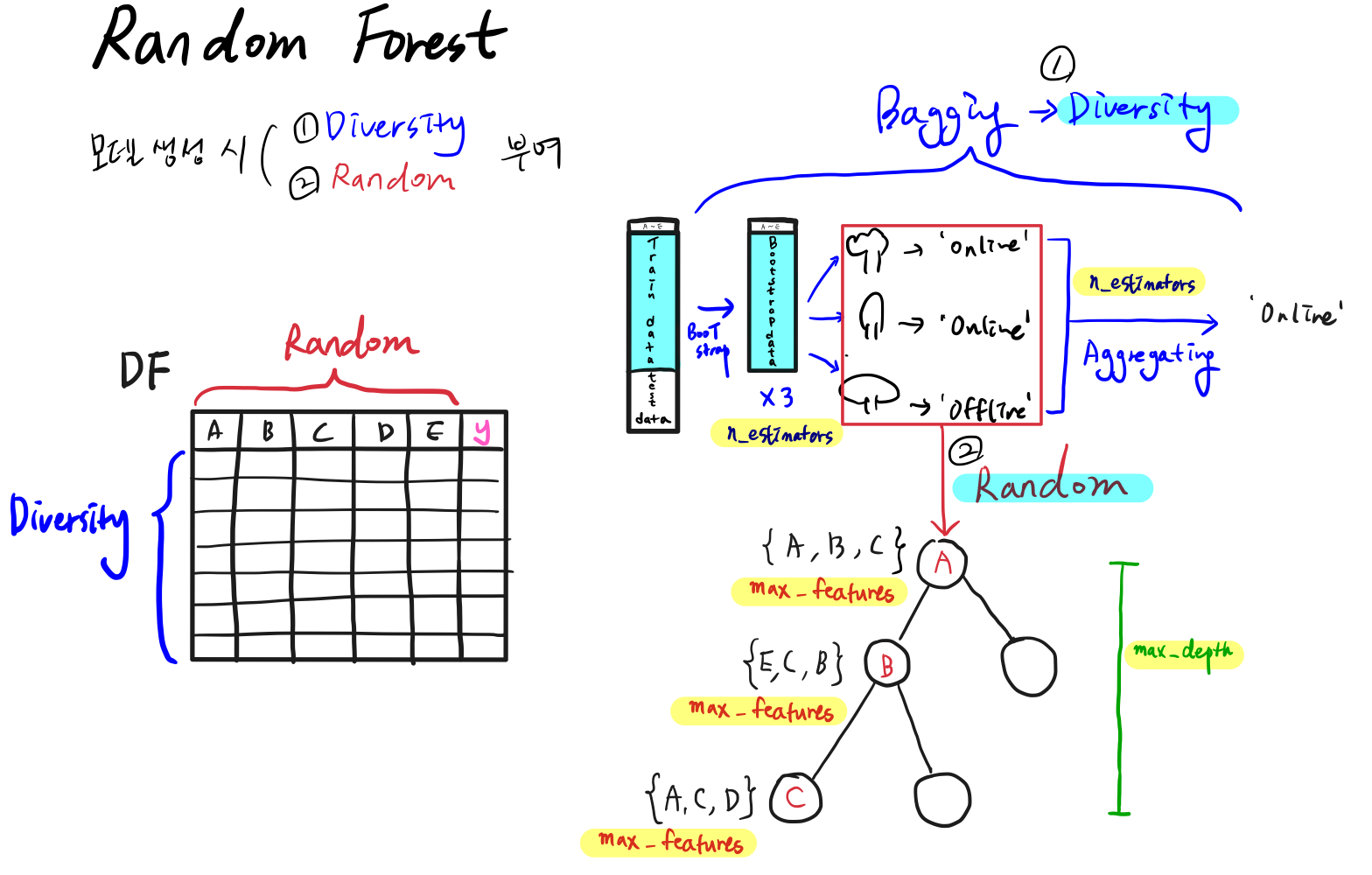
다양성(Diversity)

Bagging(Bootstrap + Aggregating)

나무를 다양하게 생성하고, 다양한 나무로부터 나온 결과들을 통합하는 것

Bootstrap

다양성을 위해 Bootstrap 방식으로 새로운 데이터를 생성함

• 원본 Data를 사용하여 여러 개의 서로 다른 Train Data를 생성함
  • 생성된 Train Data 마다 별도의 의사결정나무 모델을 생성함
  • 의사결정나무 모델 개수를 조정하기 위한 Hyperparameter : n_estimators
• Train Data는 Original Data에서 단순 복원 임의추출법으로 생성(중복이 있음)
  • 예를 들어 Original Data에 데이터포인트가 3개이고 nestimators가 3이라면,
    ($X_1, X_2, X_3$), ($X_1, X_1, X_3$), ($X_3, X_2, X_3$)으로 Train data로부터 3개의 Bootstrap Data를 생성한다.

Aggregating

다양성을 위해 여러개 Bootstrap 모델의 결과를 통합함

• Hyperparameter인 모델의 개수(n_estimators)에 따라 통합 결과가 달라짐
• 모델별 통합 방법
  • 분류 모델 : 다수결 또는 가중치를 적용하여 통합
    • $\hat{y} = (1,0,0,0,1,1,1,1,1)=1$
      *홀수로 주지 않아도, 50대 50으로 나올 경우는 매우 드물기 때문에 짝수로 주어도 됨
  • 예측 모델 : 평균값 또는 가중평균값으로 통합
    • $\hat{y} = (77,75,76,77,76)=76.2$

임의성(Random)

Random Subspace

임의성을 위해 의사결정 나무 생성 시 Feature를 무작위로 선택하는 것

• 원본 Feature에서 무작위로 입력 Feature를 추출하여 적용함(하나의 입력에 Feature 중복이 없는 비복원 추출)
• Decision Tree 보다 다양한 Feature를 활용함
• 입력 변수 개수 조정을 위한 Hyperparameter : max_features
  • default : $\sqrt{Feature\ 수}$

2) Hyperparameter

일반적으로 조정되는 파라미터는 상위 3개

종류

1. n_estimators : 모델에 사용되는 의사결정나무 개수
2. max_features : 분할에 사용되는 Feature의 개수
3. max_depth : 트리 모델의 최대 깊이
4. max_leaf_nodes : Leaf 최대 개수
5. min_samples_split : 분할을 위한 최소한의 샘플 데이터 개수
6. min_samples_leaf : Leaf가 되기 위한 최소한의 샘플 데이터 개수