[Practical Statistics] 확률(Probability)

Probability(확률)

일정 조건 하에서 어떤 사건이 발생할 가능성의 정도

• 수학적 확률 : 어떤 사람이 계산해도 동일한 값으로 계산되는 확률
• 통계적 확률 : 어떤 사건을 독립시행으로 반복했을 때 발생하는 확률
• 주관적 확률 : 관찰자의 주관에 따라 다르게 표현되는 확률

확률의 공리적 정의(일반적 정의)

‘모든 사건의 경우의 수’에 대한 ‘특정 사건’이 발생한 빈도수의 비율

• 확률 = $\cfrac{특정 사건의 원소 개수}{모든 사건의 원소 개수}$
• 확률 = Ratio(비율)
• 사건 A의 확률은 $0 \le P(A) \le 1$ 범위를 가짐
  • 공사건 : $P(\emptyset) = 0$
  • 전사건 : $P(S) = 1$
• 일반적으로 각각의 원소에 모두 같은 가중치(Weight)를 부여함

집합, 확률, 통계 용어 정리

행이 같다면 같은 개념이다(예 : 전체집합 = 표본공간 = 모집단).

집합	확률	통계
원소	원소	데이터
전체집합	표본공간	모집단
부분집합	사건	표본집단
		확률과 통계를 Binding하는 요소들 모집단분포 확률변수 확률분포 누적분포함수

• 표본공간 = 모집단 -> 모집단 분포(모집단이 따르는 확률분포)
• 사건 = 포본집단 = 확률변수
• 확률변수에 확률을 각각 대응 -> 확률분포
• 확률분포를 설명하기 위한 함수 -> 확률분포함수
• 확률 변수가 특정 값보다 작거나 같을 확률을 나타내는 함수 -> 누적확률분포함수

1) 시행

동일한 조건에서 여러 번 반복한 결과가 우연에 의해 지배되는 실험 또는 관찰

• 예 : 동전 던지기

2) 표본공간(Sample Space)

시행(통계적 실험)에서 발생 가능한 ‘모든 결과(원소)’들의 집합

• 표본공간 = 모집단
• 두 개의 동전을 던지는 실험 : S = {HH, HT, TH, TT}
• 표본공간 기호 : S

3) 사건(Event)

표본공간의 부분집합

• 사건 = 표본집단
• 두 개 동전을 던지는 실험에서 같은 면이 나오는 사건 : A = {HH, TT}
• 사건 A 기호 : A

확률적 사건

표본공간에서 ‘특정한 조건을 만족하는 결과(원소)’들의 집합

확률적 사건의 종류

• 전사건(Total Event) : S의 모든 원소를 포함하는 사건(전수조사)
• 공사건(Null Event) : S의 어떤 원소도 포함하지 않는 사건
• 여사건(Complementary Event) : 사건 A에 포함되지 않는 S의 모든 원소
• 합사건(Union Event) : 두 사건 A, B 중 적어도 한쪽에서 발생하는 사건
• 곱사건(Intersection Event) : 두 사건 A, B에 동시에 발생하는 사건
• 배반 사건(Mutually Exclusive Event) : 한 쪽에서만 발생하는 사건
• 근원사건(Fundamental Event) : 원소의 개수가 1개인 사건

4) 확률변수(Random Variable)

확률적 법칙(사건)에 따라 변화하는 값

• 확률변수 = 표본집단 = 사건
• 확률변수 기호 : X

상태공간(State Space)

확률변수가 취하는 모든 값의 집합

• 상태공간(확률변수 전체)을 구성하는 각 값이 발생하는 확률이 존재함

확률 변수의 종류

• 이산확률변수 : 확률변수가 유한하게 존재함(이산형, 셀 수 있음)
• 연속확률변수 : 확률 변수가 연속적인 구간 내 값을 취함(연속형, 셀 수 없음)

예

모집단 {1, 3, 5, 7, 9} 숫자가 적힌 5장의 카드

• 확률변수 X : 두 장의 카드를 복원추출하여 나온 숫자의 합(확률적 법칙, 사건)
• 확률변수 X = {2, 4, 6, 8, 10, 12, 14, 16, 18}

	1	3	5	7	9
1	2	4	6	8	10
3	4	6	8	10	12
5	6	8	10	12	14
7	8	10	12	14	16
9	10	12	14	16	18

5) 확률분포(Probability Distribution)

확률변수가 어떤 값을 가질지에 대한 확률
확률변수 값과 각 확률변수 값이 발생할 수 있는 확률을 대응시킨 것

확률변수 X의 확률분포표

확률 변수 X값과 각 값이 가질 확률 $P(X = x)$을 표로 표현

$X$	2	4	6	8	10	12	14	16	18
$P(X = x)$	$\cfrac{1}{25}$	$\cfrac{2}{25}$	$\cfrac{3}{25}$	$\cfrac{4}{25}$	$\cfrac{5}{25}$	$\cfrac{4}{25}$	$\cfrac{3}{25}$	$\cfrac{2}{25}$	$\cfrac{1}{25}$

6) 확률분포함수

확률변수 값이 발생할 확률을 나타내는 함수

• 특정 확률 변수의 확률분포함수를 알고 있다면
• 어떤 사건이 발생할 확률을 계산(예측) 가능하다.

확률분포함수의 종류

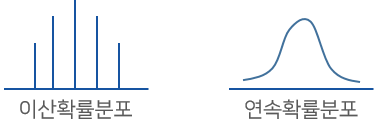
• 확률질량함수(Probability Mass Function) : $\sum F(X)$

  이산확률변수의 확률분포를 나타내는 함수

• 확률밀도함수(Probability Density Function) : $\int F(X)$

  연속확률변수의 확률분포를 나타내는 함수

https://excelsior-cjh.tistory.com/193

예

두 장의 카드를 뽑아서(이산형), 두 숫자의 합이 8이상 14이하일 확률은?

$P(8 \le X \le 14) = \cfrac{4}{25} + \cfrac{5}{25} + \cfrac{4}{25} + \cfrac{3}{25} = \cfrac{16}{25} $

7) 누적분포함수(Cumulative Distribution Function)

확률 변수 X가 특정 값보다 작거나 같을 확률을 나타내는 함수

• 분포함수 = 누적분포함수
• 확률변수 X에 대해서 확률변수 X가 특정값보다 작거나 같을 확률
• 확률밀도함수 그래프 곡선에서 아래 구간의 면적
• $F(X) = P(X \le x)$
• 전체 면적은 1

모수(Parameter)

분포함수의 모양을 결정하는 것들(예 : 평균과 분산)

누적분포함수의 종류

• 이항분포(Binomial Distribution) -> 확률질량함수, 확률밀도함수(N이 클 때)
• 정규분포(Normal Distribution) -> 확률밀도함수
• 표준정규분포(Standard Normal Distribution) -> 확률밀도함수

(1) 이항분포(Binomial Distribution)

Bernoulli’s Trial(베르누이 시행)

두 가지 결과가 나타나는 확률실험

• $p$ : 확률로 원하는 결과가 나타나면 ‘성공’
• $1-p$ : 확률로 반대의 결과가 나타나면 ‘실패’
• 모수 : 성공확률 $p$
• 확률질량함수 : $P(X = x) = F(x) = p^x(1-p)^{1-x}$

이항분포(Binomial Distribution)

성공확률이 $p$로 동일한 베르누이 시행을 $n$번 반복하여 실험

https://suhak.tistory.com/110

$B(n, p) = \dbinom{n}{k} p^x (1-p)^{n-x}$

• 시행을 $n$번 반복해도 $p$는 동일
• 독립시행
• 모수(Parameter)
  • 성공확률 : $p$
  • 시행횟수 : $n$
  • 성공횟수 : $x$

(2) 정규분포(Normal Distribution)

성공확률 0.5, 시행횟수 n이 매우 큰 이항분포는 정규분포와 비슷해 짐

https://ko.wikipedia.org/wiki/정규_분포

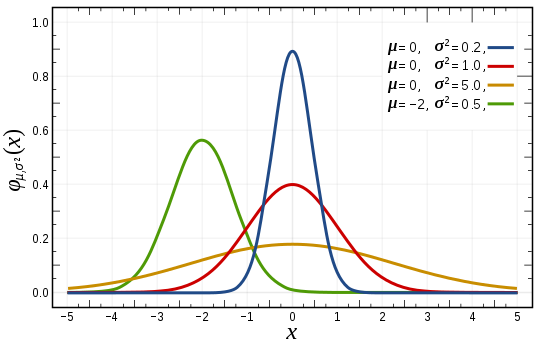
$f(x) = \cfrac{1}{\sqrt{2\pi \sigma^2}} e^{-\cfrac{(x-\mu)^2}{2 \sigma^2}}$

• 이항분포를 반복하는데, 반복 시행횟수가 매우 커지면 x가 이산형이 아닌 연속형으로 다룰 수 있게 됨
• 함수의 모양이 평균을 중심으로 좌우대칭인 종모양
• 모수(Parameter)
  • 평균
  • 분산

(3) 표준정규분포(Standard Normal Distribution)

평균 0, 분산 1인 정규분포

http://piramvill2.org/?p=3748

$ Z = N(0, 1)$

$ Z = \cfrac{X - \mu}{\sigma}$

$ f(x) = \cfrac{1}{\sqrt{2 \pi}} e^{-\cfrac{x^2}{2}}$

• 확률변수 X의 평균이 $\mu$이고, 분산이 $\sigma^2$인 정규분포를 따른다면,
• 표준 변환(Z-transform)에 의해 정규분포를 표준정규분포로 변환 가능함

(4) 기타 분포함수

t-분포(Student’s t-Distribution)

소규모 표본인 경우에 쓸 수 있는 새로운 분포
모집단이 정규분포를 따르더라도 분산이 알려져 있지 않고, 표본의 수가 적은 경우에
‘모평균’에 대한 신뢰구간 추정 및 가설검정에 사용하는 분포

• 모분산을 정확히 알 수 없기 때문에 모분산 대신 표본분산을 이용한 분포
• 표본의 크기가 30보다 작으면 t 분포를 사용해야 함(n이 30보다 크면 정규분포를 사용하여 검정)
• 자유도가 증가할 수록 표준정규분포에 가까워짐(표본수가 30이상이면 표준정규분포와 가깝다고 할 수 있음)

https://ko.wikipedia.org/wiki/스튜던트_t_분포

카이제곱분포(Chi-Squared Distribution)

k개의 정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포(표준정규분포를 제곱)
‘모분산’에 대한 신뢰구간 추정 및 가설검정에 사용하는 분포

• 자유도가 증가할수록 평균을 중심으로 좌우대칭 형태를 가짐

https://bookdown.org/mathemedicine/Stat_book/-.html#chi-square-distribution-1

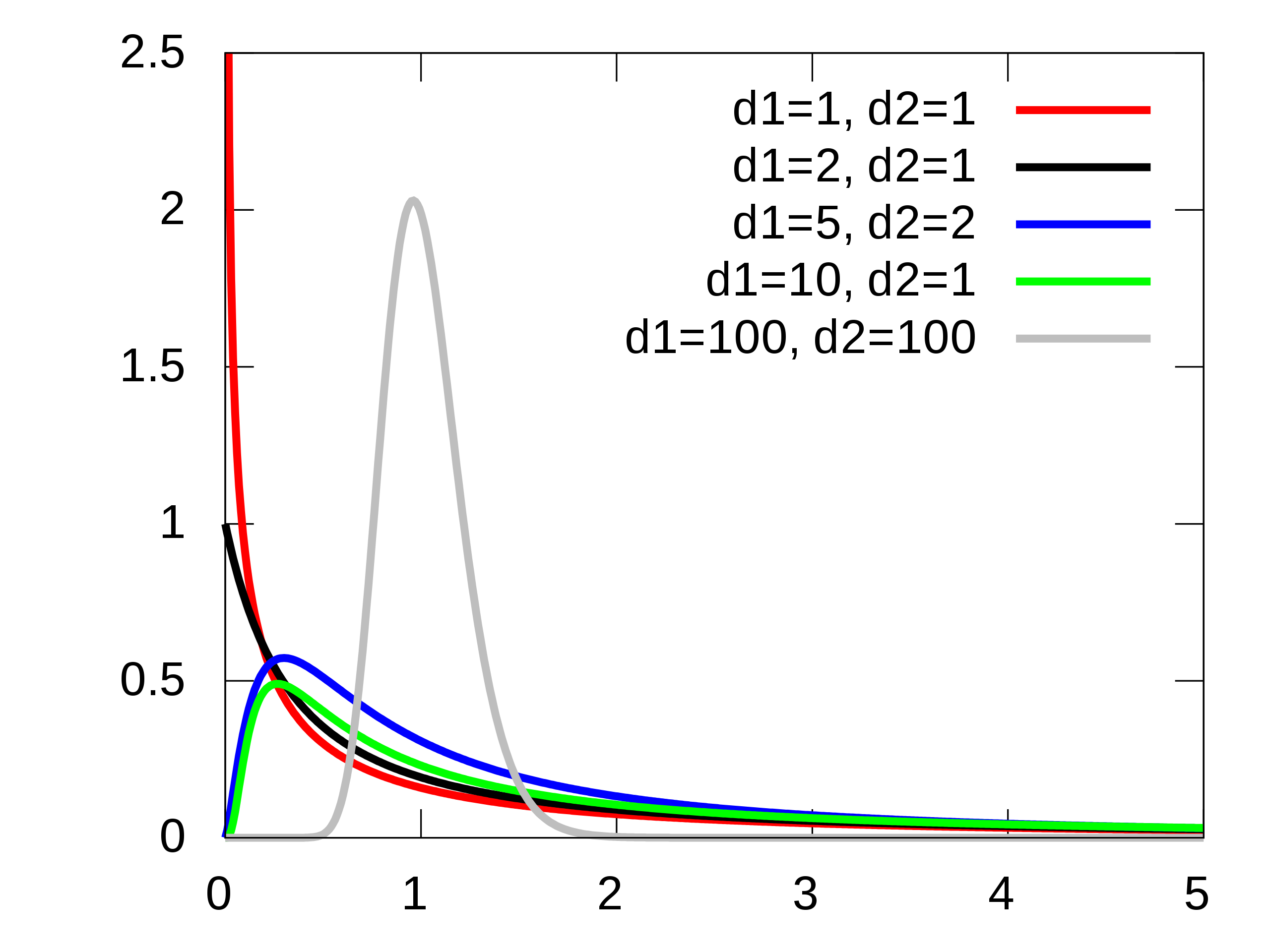
F분포(F-Distribution)

정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산 비율이 나타내는 연속확률분포
‘두 개 이상의 표본집단의 분산을 비교’하거나 ‘모집단의 분산을 추정’하기위해 사용하는 분포

• 2개 이상의 표본평균들이 동일한 모평균을 가진 집단에서 추출되었는지(또는 서로 다른 모집단에서 추출되었는지) 확인

https://ko.wikipedia.org/wiki/F_분포