[이것이 취업을 위한 코딩 테스트다] 다이나믹 프로그래밍(Dynamic Programming)

1. 중복되는 연산을 줄이자

• 컴퓨터를 활용해도 해결하기 어려운 문제는 ‘최적의 해’를 구하기에 시공간이 많이 필요한 문제이다.
• 컴퓨터는 연산속도, 메모리 공간의 한계가 있어 연산속도와 메모리 공간을 최대한으로 활용할 수 있는 효율적인 알고리즘을 작성해야 한다.

예 : 피보나치 수열(점화식)

• 점화식 : 인접한 항들 사이의 관계식
• 피보나치 수열의 점화식
  • $a_{n+2}\ =\ f(a_{n+1}, a_n)\ =\ a_{n+1} + a_n$
  • $a_n\ =\ a_{n-1} + a_{n-2}$
  • $a_1 = 1,\ a_2 = 1$
• 피보나치 수를 구하는 과정
  • $f(1), f(2)$ 함수를 반복해서 호출
  • $f(1), f(2)$를 만났을 때는 호출을 정지(재귀함수 혹은 반복문 정지 조건)
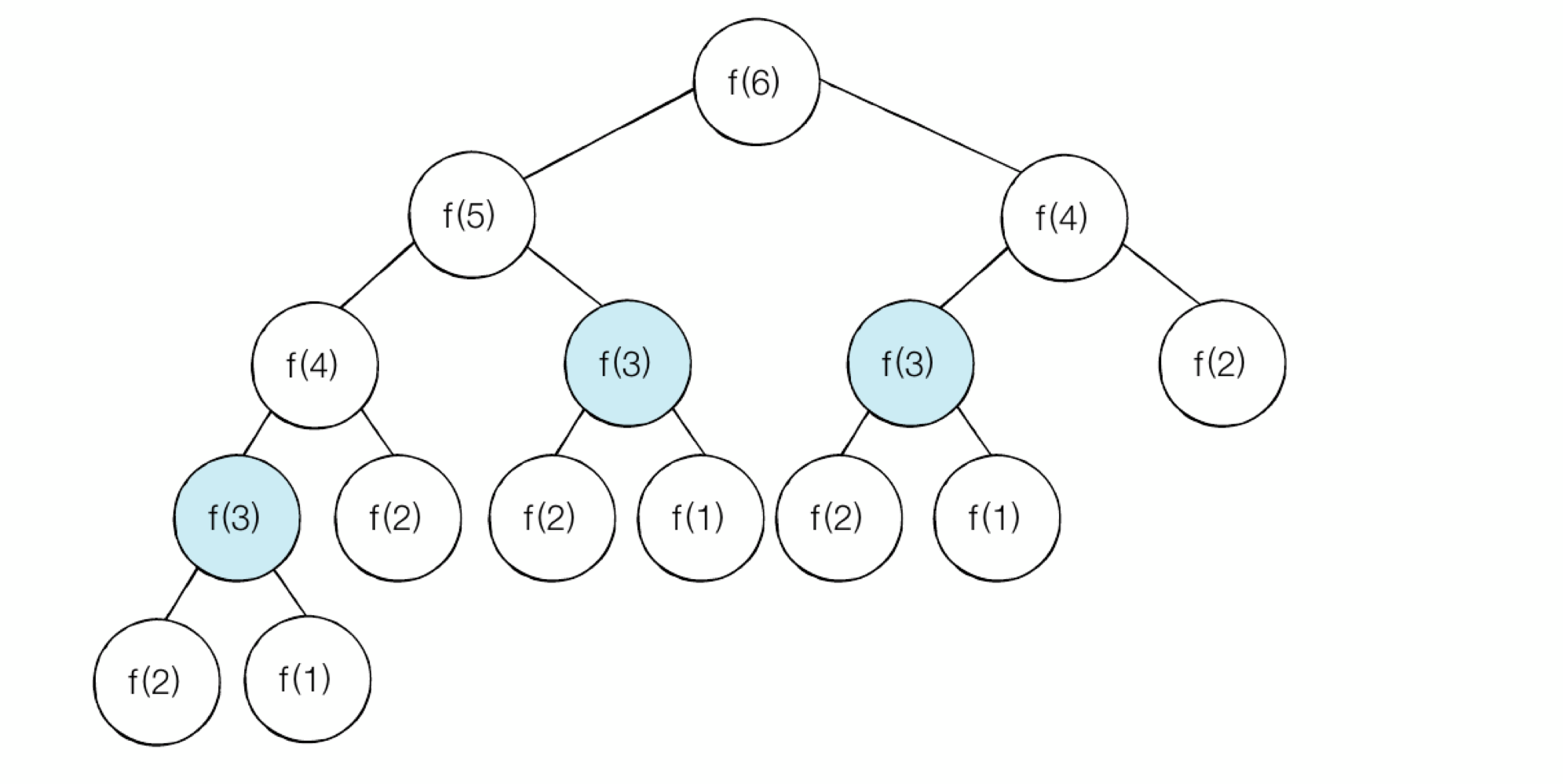
• 동일한 함수가 반복적으로 호출되므로 n이 커지면 커질수록 호출되는 수가 많아지는 문제가 있다.
• 시간복잡도 : $O(2^N)$

def fibo(x):
    if x == 1 or x == 2:
        return 1
    return fibo(x-1) + fibo(x-2)

print(fibo(4))
# 3

2. 다이나믹 프로그래밍(= 동적계획법)

• 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 기법
• 메모리 공간을 약간 더 사용하면, 연산속도를 비약적으로 증가시킬 수 있는 방법(이미 해결된 문제는 답을 저장)
• 방식은 2가지(Top-down, Bottom-up)이다.

사용 조건

• 큰 문제를 작은 문제로 나눌 수 있다.
• 동일한 작은 문제를 반복적으로 해결해야 한다.

1) Top-down(= Memoization)

• 큰 문제를 해결하기 위해 작은 문제를 호출하는 방식
• 메모이제이션(Memoization) 기법을 사용하여 해결하는 방식

메모이제이션

• 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법
• 값을 저장하는 방법이므로 캐싱(Caching)이라고도 함
• 다이나믹 프로그래밍을 구현하는 방법 중 한 종류
• 재귀함수를 사용하여 구현
  • 재귀 함수를 사용하면 오버헤드가 발생할 수 있으므로, 반복문을 사용해야함(Bottom-up)
  • sys.setrecursionlimit() 함수를 사용하여 최대 재귀 깊이를 설정하면,
  • ‘Recursion depth’ 관련 에러를 처리할 수 있다.

예 : 피보나치 수열(메모이제이션)

• 피보나치 수열 확인
• 시간복잡도 : $O(N)$

d = [0] * 100

def fibo(x):
    # 종료 조건
    if x == 1 or x == 2:
        return 1

    # 이미 계산한 적 있는 문제라면 그대로 반환
    if d[x] != 0:
        return d[x]
    
    d[x] = fibo(x-1) + fibo(x-2)
    return d[x]

print(fibo(99))
# 218922995834555169026

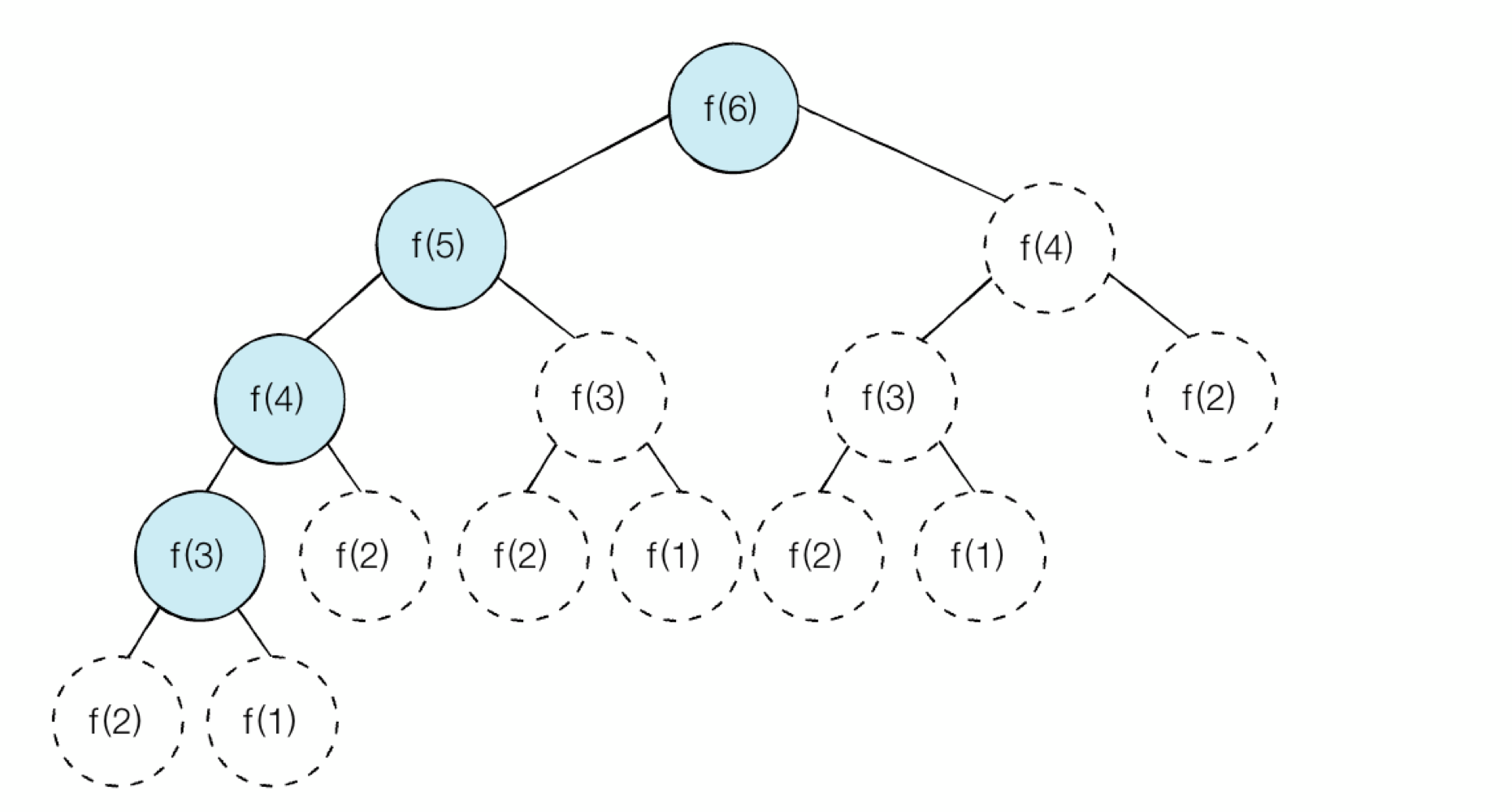
• 호출되는 함수 확인

d = [0] * 100

def fibo(x):
    print('f(' + str(x) + ')', end= ' ')
    
    if x == 1 or x == 2:
        return 1
    if d[x] != 0:
        return d[x]
    
    d[x] = fibo(x-1) + fibo(x-2)
    return d[x]

fibo(6) 
# f(6) f(5) f(4) f(3) f(2) f(1) f(2) f(3) f(4)

2) Bottom-up 반복문을 사용하여 해결

• 반복문을 사용한 방법, 다이나믹 프로그래밍의 전형적인 형태
• 다이나믹 프로그래밍은 반복문을 이용하면 성능이 더 좋다.

# DP 테이블 초기화 
d = [0] * 100

d[1] = 1
d[2] = 1
n = 99

for i in range(3, n+1):
    d[i] = d[i-1] + d[i-2]

print(d[n])
# 218922995834555169026

3. 실전 문제

1로 만들기

정수 X가 주어질 때 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지이다.

• a) X가 5로 나누어떨어지면, 5로 나눈다.
• b) X가 3으로 나누어떨어지면, 3으로 나눈다.
• c) X가 2로 나누어떨어지면, 2로 나눈다.
• d) X에서 1을 뺀다.

정수 X가 주어졌을 때, 연산 4개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

예를 들어 정수가 26이면 다음과 같이 계산해서 3번의 연산이 최솟값이다.

• 1) 26 - 1 = 25 (d)
• 2) 25 / 5 = 5 (a)

• 3) 5 / 5 = 1 (a)

• 시간 제한 : 1초
• 메모리 제한 : 128MB
• 입력 조건 : 첫째 줄에 정수 X가 주어진다. ($1 \le X \le 30,000$)

-> 그림을 그려보면 같은 함수가 동일하게 여러번 호출된다. 다이나믹 프로그래밍을 사용하면 효율적!

x = int(input())
# 26

d = [0] * 30001

for i in range(2, x + 1):
    d[i] = d[i - 1] + 1 # 현재의 수에서 1을 빼는 경우

    if i % 2 == 0: # 2로 나누어 떨어지는 경우
        d[i] = min(d[i], d[i // 2] + 1)
    if i % 3 == 0: # 3로 나누어 떨어지는 경우
        d[i] = min(d[i], d[i // 3] + 1)
    if i % 5 == 0: # 5로 나누어 떨어지는 경우
        d[i] = min(d[i], d[i // 5] + 1)
        
print(d[x])
# 3

점화식으로 표현 : $ a_i = min( a_{i-1}, a_{i/2}, a_{i/3}, a_{i/5} ) + 1$

개미 전사

개미 전사는 부족한 식량을 충당하고자 메뚜기 마을의 식량창고를 몰래 공격하려고 한다. 메뚜기 마을의 식량창고는 일직선으로 이어져있고, 개미 전사는 선택적으로 약탈하여 식량을 빼앗을 예정이다. 이때 메투기 정찰병들은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량창고가 공격받으면 바로 알아챌 수 있다. 따라서 개미 전사는 정찰병에게 들키지않기 위해 최소한 한 칸 이상 떨어진 식량창고를 약탈해야한다.

예를 들어 식량창고 4개가 다음과 같이 존재한다고 가정하자.

{1, 3, 1, 5}

이 때 개미전사는 두번째 식량창고와 네번째 식량창고를 선택했을때 최대값인 8개의 식량을 빼앗을 수 있다. 개미전사는 식량창고가 이렇게 일직선상일 때 최대한 많은 식량을 얻기를 원한다. 개미 전사를 위해 식량창고 N개에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최댓값을 구하는 프로그램을 작성하시오.

• 시간 제한 : 1초
• 메모리 제한 : 128MB
• 입력 조건
  • 첫째 줄에 식량창고의 개수 N이 주어진다. ($3 \le N \le 100$)
  • 둘째 줄에 공백으로 구분되어 각 식량창고에 저장된 식량의 개수 K가 주어진다. ($0 \le K \le 1,000$)

-> 그림을 그려보면 같은 함수가 동일하게 여러번 호출된다. 다이나믹 프로그래밍을 사용하면 효율적!

n = int(input()) 
# 4

array = list(map(int, input().split())) 
# 1 3 1 5

d = [0] * 100

d[0] = array[0] # 1
d[1] = max(array[0], array[1]) # 3

for i in range(2, n): # 2 ~ 3
    d[i] = max(d[i - 1], d[i - 2] + array[i])
#   d[2] = max(d[1]=3, d[0] + 1 = 2) = 3
#   d[3] = max(d[2]=3, d[1] + 5 = 8) = 8

print(d[n - 1])
# d[3] = 8

점화식 표현 : $a_i = max( a_{i-1}, a_{i-2} + k_i ) $ (k는 i 창고의 식량의 양)

바닥 공사

가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다. 태일이는 이 얇은 바닥을 1 $\times$ 2의 덮개, 2 $\times$ 1의 덮개, 2 $\times$ 2의 덮개를 이용해 채우고자 한다.

이 때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오. 예를 들어 2 $\times$ 3 크기의 바닥을 채우는 경우의 수는 5가지 이다.

• 시간 제한 : 1초
• 메모리 제한 : 128MB
• 입력 조건 : 첫째 줄에 N이 주어진다. ($1 \le N \le 1,000$)

n = int(input())
# 3

d = [0] * 1001

d[1] = 1
d[2] = 3

for i in range(3, n + 1):
    d[i] = (d[i - 1] + 2 * d[i - 2]) % 796796

print(d[n])
# 5

점화식 표현 : $a_i = a_{i-1} + a_{i-2} \times 2$

효율적인 화폐 구성

N가지 종류의 화폐가 있다. 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다. 이 때 각 화폐는 몇 개라도 사용할 수 있으며, 사용한 화폐의 구성은 같지만 순서만 다른 것은 같은 경우로 구분한다. 예를 들어 2원, 3원 단위의 화폐가 있을 때는 15원을 만들기 위해 3원을 5개 사용하는 것이 가장 최소한의 화폐 개수이다.

• 시간 제한 : 1초
• 메모리 제한 : 128MB

• 입력 조건 : 첫째 줄에 N, M이 주어진다. ($1 \le N \le 100,\ \ 1 \le M \le 10,000$)

• 문제 해설
  • 적은 금액부터 큰 금액까지 확인하며 차례대로 만들 수 있는 최소한의 화폐 개수 찾기
  • 금액 : $i$, 최소 화폐 개수 : $a_i$, 화폐 단위 : $k$
  • $i-k$를 만들 수 있는 최소한의 화폐 개수 : $a_{i-k}$
  • $a_{i-k}$를 만드는 방법이 존재하는 경우, $a_i = min(a_i, a_{i-k}+1)$
  • $a_{i-k}$를 만드는 방법이 존재하지 않는 경우, $a_i = 10,001$

n, m = map(int, input().split())

array = []
for i in range(n):
    array.append(int(input()))

d = [10001] * (m + 1)

d[0] = 0

for i in range(n):
    for j in range(array[i], m + 1):
        if d[j - array[i]] != 10001:
            d[j] = min(d[j], d[j - array[i]] + 1)

if d[m] == 10001:
    print(-1)
else:
    print(d[m])